| Submeter | Todas submissőes | Melhores | Voltar |
EDUPT02 - Fibonacci, quantas chamadas? |
Algumas vezes, quando você é um estudante de computação, irá ver exercícios o problemas envolvendo a sequencia de Fibonacci. Esta sequencia tem os 2 primeiros valores com 0 e 1 e cada valor seguinte é a soma dos dois números anteriores. Por definição, a fórmula para encontrar o n-ésimo número da sequencia de Fibonacci é:
fib(0) = 0
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2);
Uma forma de encontrar esse número n é usando recursão, na qual uma função chama a si mesma repetidas vezes. O esquema abaixo representa a árvore de derivação quando se calcula fib(4) ou seja, o 5 valor dessa sequencia:
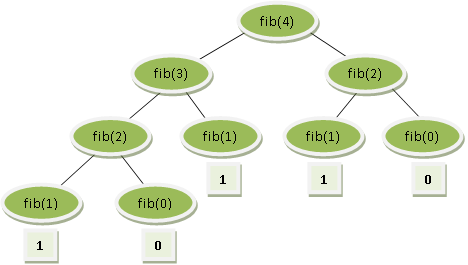
Temos então
- fib(4) = 1+0+1+1+0 = 3
- 8 chamadas recursivas foram feitas
Lembrando que o uso de variáveis globais não é uma boa prática de programação, portanto não é permitido na resolução.
Entrada
A primeira linha entrada contém um único inteiro N, indicando o número de casos de teste. Cada caso de teste contem um inteiro X (1 ≤ X ≤ 39) .
Saída
Para cada caso de teste há uma linha de saída com '\n' no final, no formato "fib(n) = F, fazendo C chamadas", onde F é o n-ésimo número da sequencia e C é o número de chamadas recursivas realizadas.
| Exemplo de Entrada | Exemplo de Saída |
|
3 |
fib(5) = 5, fazendo 14 chamadas |
| Adicionado por: | IFTM_Maratona |
| Data: | 2022-06-15 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | C C99 |
| Origem: | traduzido de Neilor Tonin |

 RSS
RSS