| Submit | All submissions | Best solutions | Back to list |
HS10DIST - Distribution of goods |
Adam's company is growing fast. Consequently, the company's storehouse and goods collection point is no longer able to serve customers smoothly. Moreover, the customers complain about the long distance and high transport costs.
Adam concerns two solutions:
- To develop his own transport service and deliver all goods to the customers' places.
- To set up new collection points.
To decide between those two opportunities Adam needs to know how much he is able to reduce the dissatisfaction of his customers by setting up k new collection points.
To evaluate the above he created the following model:
- instead of a real terrain map he will use the Carthesian coordinates with the Adam's company headquaters (d0) located in the point D0 = (0,0),
- all customers ci (1 <= i <= n <=2000) receive a weight values wi (1 <= wi <=10) in such a way that more important customers receive larger wi and the locations given by points Ci = (cix, ciy), where cix and ciy are integers
- describe each of the planned collection points: di (1 <= i <= k) will be assigned the point Di.
- As a criterion function Adam took:
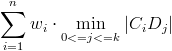 ,
,
the sum of distances from each of the customers to the nearest collection point, with customers' weights taken as coefficients.
Write a program which, for a given input, computes the best allocation of d new collection points, according to the criterion function.
Input data specification
First t - the number of test cases. Next, for each of the test cases : n, the number of customers and k, the number of new collection points. Next, n rows follow, one for each customer, describing its location: cxi, cyi and weight wi.
Output data specification
For each of the testcases, output: CASE Y [N if you do not want to solve the test]
dx1, dy1 [-1000 <= dxi, dyi <= 1000]
dx2, dy2
...
dxk, dyk
Scoring
Let s be equal to
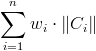 ,
,
and s' - the criterion function computed for the program output. For each test the program scores: si = s/(ks') points.
For the entire set of t tests, the program scores:
(10/t) * (s1+ s2 + ... + st) points
The total score is the sum of points scored for correctly solved test sets.
The number of points given in the ranking is scaled so that it is equal to 10 for the contestant whose solution has the highest score, and is proportionally less for all solutions with lower scores.
Example 1
Input: 3 4 1 12 -7 2 15 -1 9 12 -2 3 10 -9 8 6 2 12 -1 3 10 -9 3 13 -2 6 9 -9 7 13 -3 3 10 -9 3 8 4 4 -6 2 8 -7 4 7 -11 10 3 -6 3 6 -8 1 6 -10 3 3 -6 2 10 -7 4 Exemplary Output: CASE 1 Y 11 -8 CASE 2 Y 12 -1 10 -10 CASE 3 N Score: 136.978804
Note
The essential part of the test generator has been revealed.
Test cases has been generated with following parameters:
1 t=10, 10<=n<=20, k=2, clusters=2, 20<=cluster_range<=35; 2 t=10, 100<=n<=110, k=6, clusters=7, 5<=cluster_range<=10; 3 t=1, n=500, k=18, clusters=2, cluster_range=400; 4 t=1, n=500, k=50, clusters=6, cluster_range=250; 5 t=1, n=1000, k=3, clusters=7, cluster_range=300; 6 t=10, 30<=n<=40, k=4, clusters=4, 20<=cluster_range<=30; 7 t=10, 200<=n<=210, k=14, clusters=15, 20<=cluster_range<=30; 8 t=1, n=700 k=4, clusters=3, cluster_range=500 9 t=1, n=800, k=37, clusters=9, cluster_range=250; 10 t=1, n=2000, k=17, clusters=250, cluster_range=50;
For the first weeks of the series all submissions to this problem will be visible to all users and tested on 5 data sets only.
For the last week of the series, submissions will be visible to the submitting contestant, only, and tested on all 10 data sets. (Earlier solutions will also be extended to all 10 data sets.)
| Added by: | kuszi |
| Date: | 2010-11-08 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM32-GCC ASM64 GAWK MAWK BC C-CLANG NCSHARP CPP14 CPP14-CLANG COBOL COFFEE D-CLANG D-DMD DART ELIXIR FANTOM FORTH GOSU GRV JS-MONKEY JULIA KTLN NIM NODEJS OBJC OBJC-CLANG OCT PICO PROLOG PYPY PYPY3 PY_NBC R RACKET RUST CHICKEN SED SQLITE SWIFT UNLAMBDA VB.NET |
| Resource: | High School Programming League 2010/11 |

 RSS
RSS