| Submit | All submissions | Best solutions | Back to list |
HS09MIN - Minimal distance |
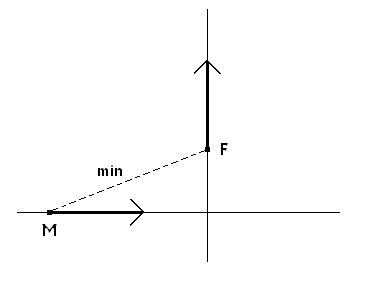
Matt and Filip love to ride a bike. Matt is currently riding west to east at constant speed VM [m/s], and Filip is riding south to north at constant speed VF [m/s]. Both of them started riding at the same time, when Matt was DM [m] before a crossroads and Filip was DF [m] past the same crossroads. Calculate the smallest distance at which Matt and Filip will be from each other during their ride.
Input
In N(2 ≤ N ≤ 60 000) lines of standard input there are four integer values VM, DM, VF, DF (2 ≤ VM, DM, VF, DF ≤ 100 000 000) separated by spaces. In line N+1 there are four zeros separated by spaces. Do not process this test case.
Output
Write out N lines to standard output. For each test case, write the minimal distance between Matt and Filip in a separate line. Preserve the order of lines from the input. The relative error of your result shouldn't exceed 0.000001
Example
Input: 17 286 34 139 12 130 9 107 31 309 22 74 38 192 26 73 29 50 27 118 0 0 0 0 Output: 317.96887
163.6
239.180354
168.66674
128.156155
Scoring
For solving this problem you will score 10 points.
| Added by: | Adam Dzedzej |
| Date: | 2009-10-17 |
| Time limit: | 0.200s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 C++ 4.3.2 CLOJURE ERL NODEJS OBJC PERL6 SQLITE VB.NET |
| Resource: | High School Programming League (thanks to Talent Association) |
hide comments
|
2010-09-24 04:15:05 Diego Alejandro Villegas Oliveros
Sorry for my English. ----------------------------------------------------- Input Vm Dm Vf Df Equations Z(X,Y)=sqrt(X^2+Y^2) → Minimice X(t)=Dm – Vm(t) Y(t)=Df + Vf(t) ----------------------- Calcule Z' Z'(X,Y)=(1/2) ((X^2+Y^2)^(-1/2)) (2X(dx/dt) + 2Y (dy/dt)) Z'(X,Y)=((X^2+Y^2)^(-1/2)) ( X(dx/dt)+Y(dy/dt)) if Z'(X,Y)=0 is a minimum value 0= X(dX/dt)+Y(dY/dt) 0= (Dm – Vm(t))(-Vm) + (Df + Vf(t)) (Vf) Obtain t t = (VmDm – VfDf)/ (Vm^2+Vf^2) If t is positive, In this time you have the minimum distance. If t is Negative when t=0 you have de minimal distance. replace t in X(t)=Dm – Vm(t) Y(t)=Df + Vf(t) and calculate the minimum value Z=sqrt(X^2+Y^2) For Java, use BigDecimal, the imput values could be 100 000 000. ----------------------------------------------- ----------------------------------------------- ----------------------------------------------- I dont understand: The relative error of your result shouldn't exceed 0.000001 Correct**********Result without result***********relative error 317.96887------->317.9688664005 163.6------------>163.6 239.180354------>239.1803535463 168.66674------->168.6667418649 128.156155------>128.1561547489 Round values Correct**********Result without result***********relative error 317.96887------->317.968866 ***X wrong answer 163.6------------>163.6 239.180354------>239.180354 168.66674------->168.666742 ***X wrong answer 128.156155------>128.156155 Someone knows, How to calcule the relative error?? Last edit: 2010-09-25 22:55:44 |

 RSS
RSS