| Submit | All submissions | Best solutions | Back to list |
DERAIL - Closing down Railway Lines |
Many cities in Byteland look back on the days when Johnny the First was king, and when nobody bothered about public spending. One of things that the citizens liked most about Johnny was that whenever he had a hangover, he would sign any public petition brought forth to him, just for the sake of peace and quiet. Rail travel was extremely popular, and lots of cities and villages requested railway lines connecting them directly, to which King Johnny always graciously agreed (even if he wasn't quite sure what he was agreeing to). Seeing that money was no object, the railway tracks were built in such a way as to connect pairs of cities directly, along straight lines. If two railroads intersected, a complex intersection involving bridges and tunnels was built and everyone seemed perfectly happy.
And then after Johnny's abdication, democracy returned, and the happy days of Byteland ended. One of the first things that had to be done was closing down most of the railway lines. The new government intends to disassemble a large part of the direct railway connections, preserving barely enough to make travel possible between any two cities (perhaps via other cities on the way). The total cost of maintenance of the lines which remain open, equal to k Bytelandian Dollars per kilometer of track open and l Bytelandian Dollars per intersection of 2 used tracks, is to be as low as possible. Please help the government decide which railroads should remain open.
Input
Input starts with a single integer t, the number of test cases (t<=100). t test cases follow.
Each test case begins with a line containing two integers n m k l, denoting the number of cities, the number of direct connections between cities, the cost of upkeep of a kilometer of track, and the cost of upkeep of a single railway line intersection, respectively (3<=n<=m<=10000, 0<=k,l<=100000). Each of the next n lines contains two integers xi yi, corresponding to the X and Y coordinates of the i-th city, measured in kilometers, respectively (-40000<=xi,yi<=40000). Then exactly m lines follow, containing a pair of integers ai bi each, which denote that cities ai and bi, numbered in input order, are connected by a direct railway track (1<=ai, bi<=n). No three cities are collinear and no three tracks intersect at one point. All tracks are bidirectional.
Output
For the i-th test case output a line containing the text case i Y or case i N, specifying whether you wish to solve the given case. Then in the former case, write exactly n-1 lines containing one integer each -- the numbers of the railway connections that ought to be left open (numbered in input order). It is guaranteed that for the input data some solution always exists.
Score
The score awarded to your program is the sum of scores received for the test cases you chose to solve. For each such test case you will receive (s/c)-1 points, where s is the cost of maintenance of the original configuration, while c is the cost of maintenance of only those railway lines which you've selected.
Example
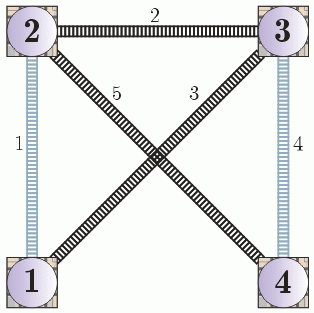
Input: 1 4 5 1 100 0 0 0 1 1 1 1 0 1 2 2 3 1 3 3 4 4 2 Output: case 1 Y 3 2 5 Score: (100+1+1+1+1.414+1.414) / (100+1+1.414+1.414) - 1 = 0.019
| Added by: | adrian |
| Date: | 2005-02-19 |
| Time limit: | 17s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | ADA95 ASM32 BASH BF C CSHARP CPP CLPS LISP sbcl LISP clisp D FORTRAN HASK ICON ICK JAVA LUA NEM NICE OCAML PAS-GPC PAS-FPC PERL PHP PIKE PRLG-swi PYTHON RUBY SCM guile SCM qobi ST TEXT WHITESPACE |
| Resource: | DASM Programming League 2004, problemset 7 |

 RSS
RSS