CAC - Cactus
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some (or perhaps all) of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex. That is, every vertex lies in the tree, but no cycles (or loops) are formed. On the other hand, every bridge of G must belong to T (a bridge is an edge whose deletion increases the number of connected components).
A spanning tree of a connected graph G can also be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices. - Wikipedia In graph theory, a cactus (sometimes called a cactus tree) is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block (maximal subgraph without a cut-vertex) is an edge or a cycle. - Wikipedia
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some (or perhaps all) of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex. That is, every vertex lies in the tree, but no cycles (or loops) are formed. On the other hand, every bridge of G must belong to T (a bridge is an edge whose deletion increases the number of connected components).
A spanning tree of a connected graph G can also be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices. - Wikipedia
In graph theory, a cactus (sometimes called a cactus tree) is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block (maximal subgraph without a cut-vertex) is an edge or a cycle. - Wikipedia
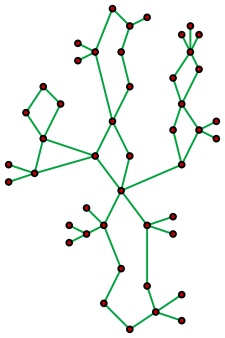
cactus graph
Your task in this problem is to count the number of ways you can convert a cactus graph to a spanning tree.
Input
The first line of input will be the number of test cases. Each test case will start with a two numbers N and E where N is the number of vertices of the cactus graph, vertices are numbered from 1 to N, 3 ≤ N ≤ 81 and E is the number of edges in the graph, 2 ≤ E ≤ 120. The next E lines each one will have two numbers v and w and that means there is an edge between vertex v and w.
Output
For each test case print “Case C: X” without quotes where C is the case number starting with 1 and X is the number of ways you can convert the given cactus graph to a spanning tree.
Example
Input: 2 3 3 1 2 2 3 1 3 5 5 1 2 2 3 2 4 3 4 4 5 Output: Case 1: 3 Case 2: 3
hide comments
|
|
ahsanul_haque:
2024-08-28 12:29:05
Just need to find all the cycle length in that graph , AC in one *.* |
|
|
jinseo0601:
2024-06-04 23:47:22
3^40 should be the maximum (i.e. 81, 120, where all simple cycles are size of 3). So unsigned long long or long double should work. |
|
|
sorin_m2:
2023-04-14 10:22:46
If you want to try the correct test from the picture above:
|
|
|
David:
2022-06-23 20:35:50
Here is the problem from the picture above!
|
|
|
depressedboy:
2021-10-26 15:26:31
Some Points To Notice
|
|
|
sonmi451:
2021-02-09 01:03:23
I struggled for this way too long, so I hope I am able to help some desperate souls:
|
|
|
zoro_swordsman:
2021-02-03 17:59:42
hey guys, i don't know what should I print in the case of an invalid input, for example, N<3 or E>120
|
|
|
sagsango:
2020-03-12 22:55:06
long long is giving WA.
|
|
|
nadstratosfer:
2019-12-23 22:34:03
Res = 1 if the graph is already a MST. WTF?! To each of you who WA'd on this stupidity and yet didn't bother to let others know, I wish you overtime on New Years eve. |
|
|
Edelweiss:
2013-05-15 12:22:39
I'm sorry to have been suspicious of test data. I'm really really sorry... please excuse me... I'll do anything you want from mee... I've also miscalculated the maximum of the result :P
|
| Added by: | hossamyosef |
| Date: | 2013-05-13 |
| Time limit: | 3s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | FCIS/ASU Local Contest 2013 |

 RSS
RSS