CFRAC - Continuous Fractions
A simple continuous fraction has the form:
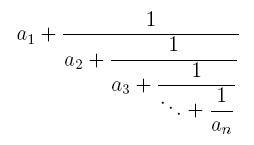
where the ai’s are integer numbers.
The previous continuous fraction could be noted as [a1, a2 ... an]. It is not difficult to show that any rational number p / q , with integers p > q > 0, can be represented in a unique way by a simple continuous fraction with n terms, such that p / q = [a1, a2 ... an−1, 1], where n and the ai’s are positive natural numbers.
Your task is to find and print the simple continuous fraction that corresponds to a given rational number.
Input
Input will consist of a series of cases, each one in a line. A line describing a case contains p and q, two integer numbers separated by a space, with 1020 p > q > 0.
The end of the input is indicated by a line containing 0 0.
Output
Cases must be analyzed in the order that are read from the input. Output for each case will consist of several lines. The first line indicates the case number, starting at 1, using the format:
Case i:
replacing i by the corresponding case number. The second line displays the input data in the
form p / q.
The remaining lines must contain the continuous fraction corresponding to the rational number p / q, specified in the given input line. The continuous fraction must be printed accordingly to the following rules:
- Horizontal bars are formed by sequences of dashes ‘-’.
- The width of each horizontal bar is exactly equal to the width of the denominator under it.
- Blank characters should be printed using periods ‘.’
- The number on a fraction numerator must be printed center justified. That is, the number of spaces at either side must be same, if possible; in other case, one more space must be added at the right side.
Example
Input: 75 34 65 60 0 0 Output: Case 1: 75 / 34 ..........1...... 2.+.------------- ............1.... ....4.+.--------- ..............1.. ........1.+.----- ................1 ............5.+.- ................1 Case 2: 65 / 60 ......1... 1.+.------ .........1 ....11.+.- .........1
hide comments
|
|
Bharath Reddy:
2014-04-04 16:18:27
Very easy problem
|
|
|
theChosenOne:
2012-08-13 19:33:03
.::Baba Ramdev::. - Weren't u supposed to be on Anshan :P |
|
|
Santiago Palacio:
2011-06-22 04:16:58
Very nice problem, i got 7 WA just for outputting bad the
|
|
|
.::Manish Kumar::.:
2011-05-23 15:55:41
@Rush what do you mean ? are p & q in the limits of LL ? |
|
|
VinyleEm:
2011-01-20 07:10:56
Again, possible to get AC without resorting to bignum implementations. Thought someone should mention that. Cheers! |
|
|
[Trichromatic] XilinX:
2009-03-21 11:35:35
After solving this problem you may try problem CFRAC2 & ACFRAC. |
| Added by: | Camilo Andrés Varela León |
| Date: | 2006-10-24 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | XX Colombian National Programming ACM 2006 |

 RSS
RSS