GRAFFTOL - King Graffs Tolls
King Graff, the ruler of the land of Feerie, feels that he is not quite rich enough. As such, he would like to impose travel tolls on his people! After all, why should they get to walk around his kingdom for free?
Feerie consists of $N$ ($1 \leq N \leq 10^5$) towns (numbered $1..N$), and $N-1$ roads. The $i$th road runs between distinct towns $A_i$ and $B_i$, in both directions. Every pair of towns is connected by exactly one path of connected roads. Currently, all travel is free, but King Graff is interested in charging for passage through certain towns.
He is planning to have a meeting with the royal computer scientist - that would be you. The meeting will last $M$ ($1 \leq M \leq 10^5$) minutes, and in the $i$th minute, one of two things will occur, described by $T_i$. If $T_i=$ "T", Graff will proclaim that town $X_i$ shall henceforth cost $Y_i$ ($0 \leq Y_i \leq 10^9$) dollars to pass through, and you'll update the map accordingly. Otherwise, if $T_i=$ "Q", he will ask you how much a trip from town $X_i$ to a different town $Y_i$ would currently cost a commoner, in order to gauge the effectiveness of his tolls - and you had better answer quickly! Note that neither the starting nor the ending town's tolls are included in a trip's cost, as they are not passed through. Note also that a town's toll may be modified by Graff mutiple times throughout the meeting, in which case the most recent modification at any point will stand.
Input
First line: 1 integer, $N$
Next $N-1$ lines: 2 integers, $A_i$ and $B_i$, for $i = 1..N-1$
Next line: 1 integer, $M$
Next $M$ lines: 1 character, $T_i$, and 2 integers, $X_i$ and $Y_i$, for $i = 1..M$
Output
$X$ lines (where $X$ is the number of questions asked by King Graff): 1 integer, the cost of the $i$th trip asked for (in dollars), for $i = 1..X$
Example
Input: 4 1 3 2 3 4 3 6 Q 1 4 T 3 5 Q 4 2 Q 3 1 T 3 1 Q 1 2 Output: 0 5 0 1
Explanation of Sample:
The map of Feerie is illustrated below:
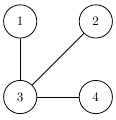
The first trip asked for by King Graff goes through towns $1 \rightarrow 3 \rightarrow 4$. Since town 3 has no toll at that point, the trip's cost is 0.
The second trip goes through towns $4 \rightarrow 3 \rightarrow 2$ and has a cost of 5, due to the new toll on town 3.
The third trip goes through towns $3 \rightarrow 1$, passing through no towns and so costing nothing.
The final trip goes through towns $1 \rightarrow 3 \rightarrow 2$ and costs only 1, as town 3's toll is reduced by then.
| Added by: | SourSpinach |
| Date: | 2013-05-12 |
| Time limit: | 3s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Own problem |

 RSS
RSS