LCA - Lowest Common Ancestor
A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. - Wikipedia
The lowest common ancestor (LCA) is a concept in graph theory and computer science. Let T be a rooted tree with N nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself). - Wikipedia
Your task in this problem is to find the LCA of any two given nodes v and w in a given tree T.
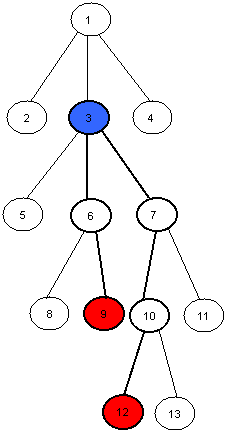
For example the LCA of nodes 9 and 12 in this tree is the node number 3.
Input
The first line of input will be the number of test cases. Each test case will start with a number N the number of nodes in the tree, 1 ≤ N ≤ 1,000. Nodes are numbered from 1 to N. The next N lines each one will start with a number M the number of child nodes of the Nth node, 0 ≤ M ≤ 999 followed by M numbers the child nodes of the Nth node. The next line will be a number Q the number of queries you have to answer for the given tree T, 1 ≤ Q ≤ 1000. The next Q lines each one will have two number v and w in which you have to find the LCA of v and w in T, 1 ≤ v, w ≤ 1,000.
Input will guarantee that there is only one root and no cycles.
Output
For each test case print Q + 1 lines, The first line will have “Case C:” without quotes where C is the case number starting with 1. The next Q lines should be the LCA of the given v and w respectively.
Example
Input: 1 7 3 2 3 4 0 3 5 6 7 0 0 0 0 2 5 7 2 7 Output: Case 1: 3 1
hide comments
|
|
cake_is_a_lie:
2017-03-02 06:05:38
I just used a single set of additional back-pointers (BIT-like) and a level tag, 0.02s. Much faster to code than <O(N), O(1)> solution. |
|
|
darshan_7807:
2016-12-06 12:02:42
LCA with RMQ |
|
|
hamjosh1:
2016-12-04 00:02:37
Node 1 is always the root :D |
|
|
xin đừng quên tôi:
2016-09-28 16:48:36
USEFUL |
|
|
priyanshu_02:
2016-07-28 19:00:09
Sparse->0.06s
|
|
|
ankurverma1994:
2016-07-27 14:56:37
O(N) pre-computation and O(sqrt(H)) per query passes :) where H is max height of tree. |
|
|
kiwi1995:
2016-07-26 17:05:03
HLD ^.^ |
|
|
iharsh234:
2016-07-16 23:29:07
My first HLD took whole day. |
|
|
darkhire21:
2016-04-19 16:20:36
try same problem on codechef for better testcases -> https://www.codechef.com/problems/TALCA |
|
|
vipul:
2016-03-30 21:23:49
done using sparse table and without sparse table.time limit is enough to get AC with complexity o(t*q*n). |
| Added by: | hossamyosef |
| Date: | 2013-05-13 |
| Time limit: | 0.600s-1.113s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | FCIS/ASU Local Contest 2013 |

 RSS
RSS