PCV3 - Problems Collection (Volume 3)
Problem 1
Using a combination of black square tiles and oblong tiles chosen from: red tiles of two units length, green tiles of three units length, and blue tiles of four units length, it is possible to tile a row of five units length in exactly fifteen different ways:
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
In how many ways can a row measuring fifty units in length be tiled?
Problem 2 A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o'clock" and numbering the tiles 2 to 7 in an anti-clockwise direction. New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings:
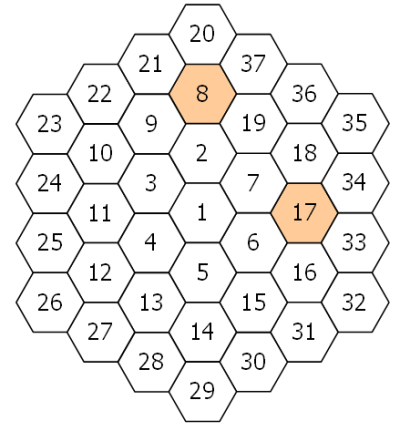
By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime.
For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3.
In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2.
It can be shown that the maximum value of PD(n) is 3.
If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271.
Find the 2000th tile in this sequence.
Problem 3
Let S(A) represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:
1) S(B) ≠ S(C); that is, sums of subsets cannot be equal.
2) If B contains more elements than C then S(B) > S(C).
For this problem we shall assume that a given set contains n strictly increasing elements and it already satisfies the second rule.
Surprisingly, out of the 25 possible subset pairs that can be obtained from a set for which n = 4, only 1 of these pairs needs to be tested for equality (first rule). Similarly, when n = 7, only 70 out of the 966 subset pairs need to be tested.
For n = 12, how many of the 261625 subset pairs that can be obtained need to be tested for equality?
Problem 4
Find the smallest integer N > 15, for which N^3 can be written using prime digits only {i.e., 2, 3, 5, 7}.
Problem 5
Let's call an integer a "titanic number" if we need 1000 or more digits to write it in decimal format. In this task you must find the minimal titanic number, which can be presented in p^q form, where p and q are prime numbers. You must output the answer in the following form: X-q, where X - the last 10 digits of the titanic number and q - the power of the exponent. For example: 8765839202-97
Problem 6
Find the smallest positive integer for which every number in the series (N-k)/k is a prime number for every k=1,...n, for n = 11. For n=4 the answer would be N=12, let's check: (12-1)/1 = 11, (12-2)/2 = 5, (12-3)/3 = 3, (12-4)/4 = 2.
Problem 7
You are playing the following game. You can ask the host of the game to tell you a number. Each number is an independent random uniformly distributed real number between 0 and 1. After the host tells you the number you can ask for more or just stop. When you stop, your score is equal to the sum of all numbers which the host has given to you. Let 0 < x < 1 and suppose that you're trying to get a score in the interval from x to 1. What is the probability of winning, assuming that you are using the best possible strategy? Find the value of probability of winning for x=0.334568 and output it after rounding in the form of *.****** - where each * denotes a digit.
Problem 8
Find the number of integers 1 < n < 10^7, for which n and n + 1 have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
Problem 9
Decode the message in the picture:

Output it with lowercase letters without spaces.
Problem 10 Suppose that you find a small program which is protected by an "activation key". The value of the key depends on the name you input. The protection for this program is performed using the code in the C programming language, presented below. The program asks you for your name and password and outputs "Accept" or "Failure".
#include <stdio.h>
unsigned int code (unsigned int arg, int p, int n)
{
unsigned int r = 1;
for(; p >= 1; p--)
r = (r*arg)%n;
return r;
}
void main ()
{
unsigned int e = 35467, n = 54031, pwd;
char name[256];
unsigned int hash, x;
printf("Name: ");
scanf("%s", name);
printf("Password: ");
scanf("%d", &pwd);
hash = 0;
for (x = 0; ; x++){
if (name[x] == 0)
break;
hash += name[x];
}
if (code(pwd, e, n) == hash)
printf("Accept!\n");
else
printf("Failure\n");
}
Your goal is to find the right passwords for each name presented in file: nicks.zip (~330 Kb). The answer for this problem will be the sum of all passwords obtained for each name from file.
Input
There is no input for this problem.
Output
Output answer as a set of lines. In each line first output the number of the problem and then the answer for this problem. If any of the answers are incorrect, you'll receive Wrong Answer.
Score
For each solved problem you'll recieve exactly one point (10 points maximum, if all problems are solved correctly).
Example
Output:
1 6174046 2 AnsweR 5 806257 8 51146700
It's just an example of what the output should look like. If all 4 answers are correct (for problems 1, 2, 5 and 8), you'll receive 4 points.
| Added by: | Roman Sol |
| Date: | 2007-07-23 |
| Time limit: | 0.100s |
| Source limit: | 10000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | TEXT |
| Resource: | ZCon 2008 |

 RSS
RSS