PHIDIAS - Phidias
Famous ancient Greek sculptor Phidias is making preparations to build another marvellous monument. For this purpose he needs rectangular marble plates of sizes W1 x H1, W2 x H2 ... WN x HN.
Recently, Phidias has received a large rectangular marble slab. He wants to cut the slab to obtain plates of the desired sizes. Any piece of marble (the slab or the plates cut from it) can be cut either horizontally or vertically into two rectangular plates with integral widths and heights, cutting completely through that piece. This is the only way to cut pieces and pieces cannot be joined together. Since the marble has a pattern on it, the plates cannot be rotated: if Phidias cuts a plate of size A ? B then it cannot be used as a plate of size B ? A unless A = B. He can make zero or more plates of each desired size. A marble plate is wasted if it is not of any of the desired sizes after all cuts are completed. Phidias wonders how to cut the initial slab so that as little of it as possible will be wasted.
As an example, assume that in the figure below the width of the original slab is 21 and the height of the original slab is 11, and the desired plate sizes are 10 x 4, 6 x 2, 7 x 5, and 15 x 10. The minimum possible area wasted is 10, and the figure shows one sequence of cuts with total waste area of size 10.
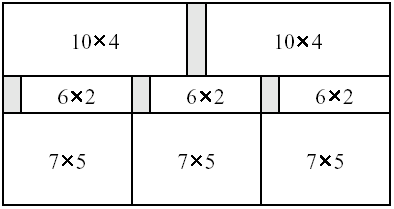
Your task is to write a program that, given the size of the original slab and the desired plate sizes, calculates the minimum total area of the original slab that must be wasted.
Input
t - the number of test cases, then t test cases follow [t ≤ 20].
The first line of each test case contains two integers: first W, the width of the original slab, and then H, the height of the original slab. The second line contains one integer N: the number of desired plate sizes. The following N lines contain the desired plate sizes. Each of these lines contains two integers: first the width Wi and then the height Hi of that desired plate size (1 ≤ i ≤ N). [1 ≤ W ≤ 600, 1 ≤ H ≤ 600, 0 < N ≤ 200, 1 ≤ Wi ≤ W, and 1 ≤ Hi ≤ H.]
Output
For each test case output one line with a single integer: the minimum total area of the original slab that must be wasted.
Example
Input: 1 21 11 4 10 4 6 2 7 5 15 10 Output: 10
hide comments
|
|
abhi_8:
2023-08-29 09:06:12
The biggest hint that is not understandable from question for poor guys like me is that, when you cut the plate along one direction, you cut as whole, you can't stop in between, 5x3 can be cut in two segments where both have same height or same width. like ( 1x3 and 4x3 ) or ( 5x1 and 5x2 ) or any such combos. This the difference with the classic tiling problem. |
|
|
evang12:
2022-01-06 23:08:27
Great problem! The problem seemed very difficult at first, but with a few observations, this problem breaks down into a much simpler one. |
|
|
an09mous:
2020-04-01 14:33:56
Interesting problem. It's not similar to the tiling problem, so don't get confused. |
|
|
sagar_maktha:
2019-09-25 20:39:50
Can anyone provide test cases?
|
|
|
adist98:
2019-07-18 02:32:01
Interesting question. |
|
|
hello_world123:
2018-06-14 21:26:25
Similar to floor tiling problem ...
|
|
|
aman_sachin200:
2018-06-13 13:28:55
Awesome one!!My 150th :P |
|
|
ayush_1997:
2017-02-26 10:25:28
nice dp :) |
|
|
lt:
2016-04-21 15:27:22
Wrong answer!!!
|
|
|
minhthai:
2016-02-23 00:13:36
thanks for the time limit for java :) nice problem |
| Added by: | Roman Sol |
| Date: | 2005-05-20 |
| Time limit: | 21s |
| Source limit: | 30000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | IOI 2004 |

 RSS
RSS