RDNWK - Road Network
In a country of N cities, the government would like to develop a new system that can answer drivers’ queries to find the shortest path between 2 cities in the country road network. However, some cities are more exciting than others, and drivers would prefer driving through them. Last month, a voting for the most exciting cities in the country was conducted, and a ranking of the P most exciting cities has been made. The government decided to utilize this ranking so that drivers can find the shortest path between 2 cities that only goes through the first K cities of the ranking as intermediate cites on the road. Hence, the query is defined as: the source city, the destination city, and K for the first K cities from the ranking. (Note that some cities may not be exciting at all, and so they will not be included in the ranking, i.e. P ≤ N)
Given undirected graph representing the country cities, and ranked list of exciting cities, you are to answer Q queries, each one asking for the shortest path between 2 cities utilizing only the first K cities from the ranked list.
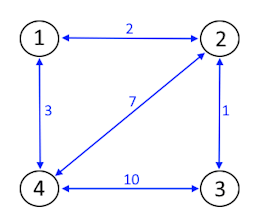
For example, given the graph in the sample (4 cities and ranked list [2 1])
- 1 - Query (k = 0, Src = 3, dest = 4): means no cities to use as intermediate, hence only direct path allowed 3-4 with cost 10.
- 2 - Query (k = 1, Src = 3, dest = 4): means we can use first city on list (2), hence we can choose between paths (3-4, 3-2-4) path 3-2-4 with cost 8 is best.
- 3 - Query (k = 2, Src = 3, dest = 4): means we can use first 2 cities on list (1, 2), hence we can choose between paths (3-4, 3-2-4, 3-2-1-4) path 3-2-1-4 with cost 6 is best.
Input
The first line of input contains an integer T that represents the number of test cases, then follow T test cases, each in following format:
Line 1 - N (1 ≤ N ≤ 150), the number of cities of the country.
N-1 lines follow, where ith line represents ith-city connection costs, Ci,j is the cost of edge (i, j), if there is no edge between i, j then Ci, j = -1 else 1 ≤ Ci,j ≤ 10000.
C1,2 C1,3 ... C1,N
C2,3 C2,4 ... C2,N
...
CN-1,N
Line N+1 - P (0 ≤ P ≤ N), represents the size of ranked list.
Line N+2 - P space-separated list of distinct cities ids (1 ≤ city id ≤ N)
Line N+3 - Q (1 ≤ Q ≤ 6000), represents the number of queries.
Q lines follow
K source destination
...
Note that: 0 ≤ K ≤ P, 1 ≤ source, destination ≤ N.
Output
For each test case, output a single line of output in the form "Case K: A1 A2 ... Aq" where K is the number of the test case and [A1 A2 ... Aq] are the answers for the Q queries. Each answer is the shortest path cost between the 2 given cities using the first only K cities of given list as intermediate cities. In case there is no path between 2 cities, the answer is -1.
Example
Input: 1 4 2 -1 3 1 7 10 2 2 1 3 0 3 4 1 3 4 2 3 4 Output: Case 1: 10 8 6
hide comments
|
|
vas14:
2022-07-30 04:32:34
To re-phrase the ambiguously stated problem, you're allowed to only use source, destination, and the first K ranked cities in the resulting path for each query. |
|
|
glays:
2017-07-14 13:26:52
O(Q * N^3) ?! With Q=6000 and N=150 ?
|
|
|
rohit9934:
2017-07-12 17:48:00
Floyd Warshall Works fine.
|
|
|
hodobox:
2017-02-23 15:31:28
My complexity is slightly worse than O(T*N^3), still had no problems (won't say exactly cause I think it spoils the problem somewhat) |
|
|
nada elnokaly:
2013-09-17 10:46:04
5s o.O ! my code with complexity O(T*N^3) gives TLE ! |
| Added by: | Mostafa Saad Ibrahim |
| Date: | 2011-11-13 |
| Time limit: | 2.426s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | 10th Egyptian Collegiate Programming Contest |

 RSS
RSS