RPLK - Kind and gently
Giselle is working on her house, as her husband won't be able to help in the task, she gently asks you for help, the task is very simple, Giselle wants to build some stairs that communicate two floors in the house. The stairs will be made of W segments of wooden, she is very confident on building the stairs, but she wants to build the stairs with some separation between steps. As you know, the end of a step is overlapped by the beginning of the other, and so on, between steps there are a single separation, as Giselle is very conservative, she wants to build the stairs using at most W segments of wood.
The image will help you to understand the task.
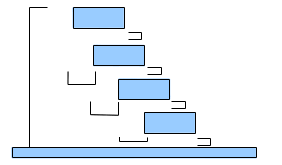
As you can see in the image, there is a single separation between each step relating to the height and the width of every step.
Giselle wants to build stairs using E pieces of wood that she wants to cut into at most W steps. You can only cut vertically and can't rotate the given pieces. Each step's width must be exactly M+1. M is the overlap and 1 is a constant width for placing feet.
Input
The first line of the test data will start with an integer T representing the T test cases, then, T cases will follow.
Each case starts with four positive integers (E, M, K, W) denoting E pieces of wood, M meters of overlap, K height of separator between each step and W, the maximum number of steps that can be cut out. Next, E lines will follow, each with two integers Eh and Ew representing respectively the height and the width of each piece of wood Giselle has.
Output
You must output the string "Scenario #i: " where i is the number of test case you're analyzing (starting at 1), followed by the maximum amount of height that you can possibly build.
Example
Input: 3 5 1 1 3 6 2 5 10 4 20 3 15 1 1 3 1 0 5 3 15 2 20 1 60 2 1 1 25 15 10 12 10 Output: Scenario #1: 19 Scenario #2: 15 Scenario #3: 145
Explanation of the First Case
You can only cut the segment of width 6 into one piece, but the 5 segment of width 10 you can cut it into 5 pieces, as you only need 3 pieces to use, the maximum height will be of 6+5+5+3 = 19
Constraints
(1 <= Width and Height of each wooden piece <= 1000) = "WiHi".
Small input (40%)
- 1<= T <= 200
- 1<= {E, K, M} <= 100
- WiHi <= M <= 100
- 1<= W <=100
Large Input (60%)
- 1 <= T <= 10
- 1 <= {E, K} <= 100,000
- WiHi <= M <= 1,000
- 1 <= W <= 10,000
hide comments
|
|
hodobox:
2015-12-15 10:24:59
O(E log E) passes, but there actually exists a O(E + constant) solution which is much faster :) |
|
|
Himanshu Srivastava:
2012-07-01 09:09:01
why i am getting TLE i used O(E log E) soln........ |
|
|
Alex Anderson:
2012-06-26 01:23:57
My algorithm is O(E log E). Is the intended solution better?
|
| Added by: | david_8k |
| Date: | 2012-06-22 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Own Problem used for the RPL contest |

 RSS
RSS