SOMESUMS - Some Sums
After giving a heart-warming, inspirational speech to the sorority sisters of Delta Gamma at the University of Maryland, Michael Shannon was assaulted on the street by an armed mathematician, who defined a function f as follows:
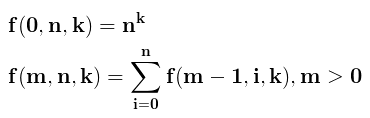
The mathematician presented Shannon with an ultimatum: You will write a program to calculate this function modulo 109+7 for various values of m, n, and k within the given constraints XOR I will shoot you with this gun!
As the mathematician lay recovering in his hospital bed, a Sigma Nu brother who had witnessed the event gingerly approached him and said, "Professor Martinson, I've written a program to solve your problem, but the online judge on your website keeps telling me the answer is wrong. Please tell me what the problem is. Submission ID 571972597."
Wearily, Martinson replied, "Have you written a brute force program to verify your program's output for smaller cases?"
The Sigma Nu brother replied, "Sorry, what did you say? I wasn't listening. Hey, are you going to eat that?" He then took the professor's chocolate pudding and went home to his lovely girlfriend from Zeta to enjoy the rest of the evening.
Input
In the first line, an integer T, the number of test cases. Then T lines containing integers m, n, and k separated by spaces.
Output
T lines containing the value of f(m, n, k) modulo 109+7 for each test case.
Constraints
1 ≤ T ≤ 20000
0 ≤ m ≤ 1000
0 ≤ n ≤ 109
0 ≤ k ≤ 1000
Example
Input: 5 0 0 0 1 100 1 2 100 0 2 100 1 100 100 100 Output: 1 5050 5151 171700 143422859
Additional Info
There are two randomly generated data sets, one with T = 10000 and the other with T = 20000. The distributions are close to uniform random.
At the time of publication, my C code runs in 0.69s and my Python 2.7 code runs in 24.70s. The Python code is about 1KB, not golfed.
hide comments
|
|
nacly_fish:
2022-06-27 13:44:55
It would be more interesting if m,k ≤ 1e7. |
|
|
David:
2021-10-29 19:27:46
After writing brute force checked for corner cases, my solution is TLE! I need a new approach.
|
|
|
Abhishek:
2015-01-05 14:16:02
isn't this Riemman's Zeta function with negative s , summed over 1->n ? |
|
|
Francky:
2014-06-13 02:18:59
Very nice problem. Now we'll have to mix SOMESUMS and MOON2. :p
|
|
|
Mitch Schwartz:
2014-06-08 04:15:24
I had the idea for this problem about two years ago but only got around to publishing now. I hope you'll enjoy my first non-BF classical problem! |
| Added by: | Mitch Schwartz |
| Date: | 2013-10-20 |
| Time limit: | 20s-30s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Generalisation of ASUMHARD |

 RSS
RSS