TAP2013A - On the side of the road
On the side of the road, there are palm trees, there's a bar, there's shadow, there's something more. In this problem, we are particularly interested in the palm trees.
Ana, Adan, Alan and Amanda organized a trip: while Ana and Adan where dealing with petty things like checking the car, preparing the luggage and finding a place to stay, Alan and Amanda dedicated themselves to the most important part: studying the views of palm trees to which they would have access to while on the road.
The road they are now driving on is completely straight, and in this problem we will represent it by the Y = 0 line of the XY plane. On the side of the road with coordinates Y > 0 there are palm trees, which we will represent by different points of the XY plane with positive Y coordinate. Alan and Amanda have noticed that from each point on the road certain palm trees are visible, and in general these vary along the road. A palm tree is said to be visible from a point on the road if and only if the segment that joins both points does not go through any other palm tree.
In the following figure the unfilled circles represent palm trees in the first sample input, whereas the filled ones represent some possible points on the road.
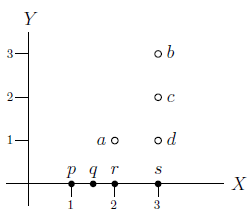
From point p the palm trees that are visible are a, b and d, since palm tree c is hidden behind palm tree a. From point q the visible palm trees are a, c and d, since palm tree b is now hidden behind palm tree a. From point r all the palm trees are visible, and from point s only palm trees a and d are visible, since palm trees b and c are hidden behind palm tree d.
While Ana and Adan take turns to drive the car, Alan and Amanda discuss the benefits of knowing how many visible quantities of palm trees there are. Given a set of palm trees, an integer number m is a visible quantity of palm trees if and only if there exists at least one point on the road (i.e. a point with coordinate Y = 0) from which exactly m palm trees are visible.
In the example illustrated above, 2, 3 and 4 are visible quantities of palm trees, as can be respectively testified by points s, p and r on the road. On the other hand, 0 and 1 are not visible quantities, because from every point of the road at least 2 palm trees are visible. Finally, no m > 4 is a visible quantity, since there are only 4 palm trees in total. Therefore, in this example there are 3 visible quantities of palm trees. (Note that if m is a visible quantity of palm trees, there could be more than one point on the road that testifies to this situation; in the previous example this is the case with points p and q for the visible quantity 3, as well as with infinitely many other points along with r for visible quantity 4.)
Ana and Adan are getting tired. They want Alan and Amanda to let go of the palm trees and at least prepare some sandwiches. For that reason, you need to make a program to calculate how many different visible quantities of palm trees there are along the road.
Input
The first line contains an integer number N indicating the number of palm trees that there are on the side of the road (1 ≤ N ≤ 1000). Each of the following N lines describes a different palm tree using two integer numbers X and Y, representing the coordinates of said palm tree in the XY plane (1 ≤ X, Y ≤ 105). There are no two palm trees that share the same position.
Output
Print a single line containing an integer number representing the number of visible quantities of palm trees that there are along the road.
Example 1
Input:
4
2 1
3 1
3 2
3 3
Output:
3
Example 2
Input: 7 2 1 3 1 4 1 1 2 3 2 5 2 3 3 Output: 4
| Added by: | Fidel Schaposnik |
| Date: | 2013-10-07 |
| Time limit: | 1s-2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | Argentinian Programming Tournament 2013 |

 RSS
RSS