TOUGH - Bits. Exponents and Gcd
Rastas's has been given a number n. Being weak at mathematics, she has to consider all the numbers from 1 to 2n - 1 so as to become perfect in calculations. (You can assume each number is consider as a soldier).
We define the strength of number i as the number of set bits (bits equal to 1) in binary representation of number i.
If the greatest common divisor of numbers a and b is gcd(a, b),
Rastas would like to calculate the function S which is equal to: 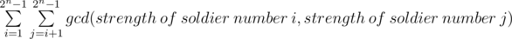
As the friend of Rastas, it's your duty to calculate S modulo 109 + 7.
Input
The first line of the input contains the number of test cases, T. Each of the next T lines contains an integer n, as mentioned in the question.
Output
For each value of n given, find the value of the function S.
Constraints
Sum of n over all test cases doesn't exceed 2500.
Example
Input: 3 1 2 5 Output: 0 3 680
hide comments
|
|
adi100:
2019-05-23 16:40:50
Nice Problem, enjoyed solving it. |
|
|
azam_9:
2016-02-06 07:34:14
getting tle..any suggestions??
|
|
|
(Tjandra Satria Gunawan)(曾毅昆):
2016-02-06 00:10:28
Nice math problem ;-) |
| Added by: | likecs |
| Date: | 2016-02-05 |
| Time limit: | 1s |
| Source limit: | 10000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 GOSU JS-MONKEY |
| Resource: | Own problem |

 RSS
RSS