In the traditional game of Musical Chairs, N + 1 children run around N chairs (placed in a circle) as long as music is playing. The moment the music stops, children run and try to sit on an available chair. The child still standing leaves the game, a chair is removed, and the game continues with N children. The last child to sit is the winner.

In an attempt to create a similar game on these days' game consoles, you modify the game in the following manner: N Children are seated on N chairs arranged around a circle. The chairs are numbered from 1 to N . Your program pre-selects a positive number D . The program starts going in circles counting the children starting with the first chair. Once the count reaches D , that child leaves the game, removing his/her chair. The program starts counting again, beginning with the next chair in the circle. The last child remaining in the circle is the winner.

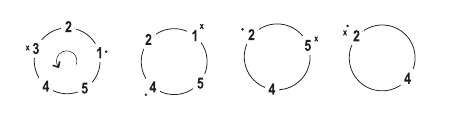
For example, consider the game illustrated in the figure above for N = 5 and D = 3 . In the figure, the dot indicates where counting starts and × indicates the child leaving. Starting off, child #3 leaves the game, and counting restarts with child #4. Child #1 is the second child to leave and counting restart with child #2 resulting in child #5 leaving. Child #2 is the last to leave, and child #4 is the winner. Write a program to determine the winning child given both N and D .

Input

Your program will be tested on one or more test cases. Each test case specifies two positive integers N and D on a single line, separated by one or more spaces, where N, D < 1,000,000 .

The last line of the input file contains two 0's and is not part of the test cases.

Output

For each test case, write the winner using the following format:

N D W

Where N and D are as above, is a space character, and W is the winner of that game.

Example

Input:
5 3
7 4
0 0

Output:
5 3 4
7 4 2

---

hide comments

< Previous 1 2 Next >
	cake_is_a_lie: 2017-02-28 03:39:54 I don't know why people get TLE on this; a fairly brute force O(N) approach gives me 0.09s. Also, in case you were still wondering, the recursive solution gives you SIGSEGV because you're putting O(N) frames on the stack and N can be 1000000. Last edit: 2017-02-28 03:42:59
	alias_9854: 2016-12-08 17:07:01 i used linked list, but it is giving runtime error! what could be the probable error,please help.
	karthik1997: 2016-06-11 10:16:30 Linked List approach fails => O(N * Log(base d)N ) approach gives TLE Josephus Recursive Fails Josephus Iterative ? Well My friend , Its upto you to decide.... :p
	galloska: 2015-08-20 00:23:13 I solved it using BIT, but that's not the best option to solve it... In live archive you get TLE if you use BIT or Segment Tree. Can someone explain me, how can I do this with DP?
	shravinson: 2015-07-17 09:31:00 can i use linked list to solve this problem???
	[Mayank Pratap]: 2015-06-07 17:23:05 Had a hard time understanding .....Finally AC :)
	Steven Hans Limantoro: 2015-06-06 12:24:27 Hint : Josephus problem (iterative version) Recursive version will lead to stack overflow Enjoy! :)
	farziengineer: 2015-05-27 11:43:48 there was a question on spoj by the name anarch(maybe),[required some bitwise implementation.], but now i cant find that question on spoj, please help
	i_am_looser: 2015-05-11 14:15:07 Solved using segment tree but it took 2 hours to implement ....
	Gaurav chandel: 2015-02-28 12:13:35 @Ankit recursion will lead to stack overflow. Use iterative version :)